Jay Menon

Robotics @ ASU

This project develops a bio-inspired soft-bodied robot mimicking inchworm locomotion using metachronal gaits. It integrates mathematical modeling, robust control, and digital twin synchronization to enable adaptive locomotion over rough and constrained terrain.

Mechanical Design and Simulation Environment

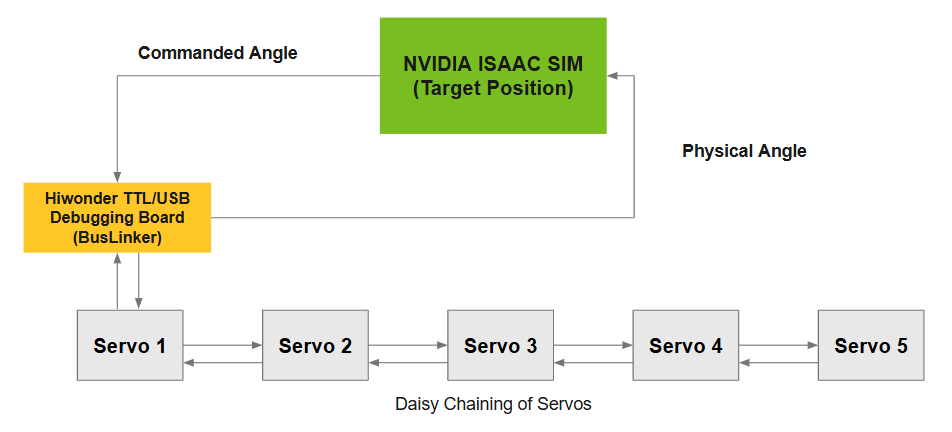
The worm robot features five rotary joints actuated by LX-16A servos (240° range) daisy-chained via TTL communication. The physical design was created in SolidWorks and exported to NVIDIA Isaac Sim via Universal Scene Description (USD). The digital twin runs in real time, receiving servo angle commands and providing visual feedback and trajectory validation.

Kinematics and Gait Generation

Forward and Inverse Kinematics were formulated using geometric algebra:

  • Rotor Algebra: Rotations represented via bivectors (e.g., R = e^(θ/2 * e1e2))
  • Motor Algebra: Unification of translation and rotation in screw theory.
  • Metachronal Gait Constraint:

Gait 1: θ₁ = 0, θ₂ = +θ, θ₃ = -θ, θ₄ = -θ, θ₅ = +θ Gait 2: θ₁ = +θ, θ₂ = -θ, θ₃ = -θ, θ₄ = +θ, θ₅ = 0

  • Net Displacement Equation: η = 2l(1 - cos(θ))

Inverse kinematics was validated in Isaac Sim by enforcing symmetry and boundary constraints on the head and tail.

Defense Presentation

Dynamics Modeling

Using Euler-Lagrange Formalism for a 5-DOF serial chain:

M(θ)·θ̈ + C(θ, θ̇)·θ̇ + G(θ) = τ

Where:

  • M(θ) ∈ ℝ⁵ˣ⁵: Mass matrix
  • C(θ, θ̇) ∈ ℝ⁵ˣ⁵: Coriolis/centrifugal matrix
  • G(θ) ∈ ℝ⁵ˣ¹: Gravity vector
  • τ ∈ ℝ⁵ˣ¹: Joint torques

Clifford Algebra & Motor Algebra:

  • Twists and wrenches represented as multivectors
  • Joint lines modeled as bivectors; moments and forces treated geometrically
  • Recursive Newton-Euler formulation expressed in algebraic multivector form

Control Strategies

PD Control

τ = Kp·e(t) + Kd·ė(t)

  • Kp = 0.7, Kd = 0.009

PID Control

τ = Kp·e(t) + Ki·∫e(t)dt + Kd·ė(t)

  • Kp = 2.0, Ki = 0.5, Kd = 0.01

Fractional PID Control (FPID)

τ = Kp·e(t) + Ki·D^{-λ}e(t) + Kd·D^μe(t)

  • λ = 0.9, μ = 0.8

Sliding Mode Control (SMC)

s = ė + β·e, τ = -Ks·sign(s)

  • Ks = 3.0, β = 6.5

Koopman-PID Control

  • Koopman operator K transforms nonlinear dynamics to lifted linear space:

z_{k+1} = K·z_k τ = PID(z_k)

  • Neural network learns K; PID control operates on lifted state z.

Video Demo

Digital Twin Implementation

  • TTL/USB BusLinker connected to real robot streams joint angles to simulation.
  • Isaac Sim receives desired trajectories; logs commanded vs actual angles.
  • Servo positions, sensor data, and gait transitions validated in simulation.

digital-twin

Video Demo

Video Demo

Sensor Integration and Extensions

  • Ultrasonic range sensor mounted on the head for obstacle awareness.
  • Step-climbing motion validated via both physical robot and digital twin.

Video Demo

Thesis

Source Code

GitHub Repo